Nathan S. Hogaboom1,2, Yen-Sheng Lin3,4, Lynn A. Worobey2,5, Alicia M. Koontz1,2, Michael L. Boninger2,6
1. Department of Rehabilitation Science and Technology, University of Pittsburgh, Pittsburgh, PA
2. Human Engineering Research Laboratories, VA Pittsburgh Healthcare System, Pittsburgh, PA
3. Sensory Motor Performance Program, Rehabilitation Institute of Chicago, Chicago, IL
4. Department of Physical Medicine & Rehabilitation, Northwestern University, Chicago, IL
5. Department of Physical Therapy, University of Pittsburgh, Pittsburgh, PA
6. Department of Physical Medicine & Rehabilitation, University of Pittsburgh, Pittsburgh, PAABSTRACT
Twenty-six wheelchair users with spinal cord injuries participated in this cross-sectional, repeated-measures study. The objective was to investigate differences in wrist joint forces and motions between users with paraplegia and tetraplegia during overground propulsion. A secondary objective was to evaluate group differences over surfaces and speeds experienced in the built environment. Participants with tetraplegia propelled with higher peak forces and flexion/extension ranges of motion (ROM). Differences were greatest during conditions that induced higher rolling resistances – carpet at unnatural propulsion speeds. These biomechanical differences are likely adaptations needed to overcome hand and wrist paralysis and could lead to secondary injury. Interventions such as orthotics or wheelchair modifications that optimize wrist biomechanics may reduce the risk of upper-extremity injury in individuals with tetraplegia; further development and testing of such interventions is warranted.
Introduction
Wrist and hand repetitive strain injuries occur after chronic exposure to repetitive, forceful hand motions in awkward wrist postures (Barr, Barbe, & Clark, 2004). Wheelchair users with spinal cord injury (SCI) often place high loads on their wrists to perform activities of daily living such as propulsion; this activity also involves large and often extreme movements of the wrist (Boninger, Cooper, Robertson, & Rudy, 1997). Thus, it is no surprise that a high prevalence of wrist and hand pain exist in this population (Pentland & Twomey, 1994).
Wheelchair users with SCI adapt to their level of injury by altering propulsion biomechanics (Newsam, et al. 1999). Previous studies, however, have reported conflicting results with respect to wrist biomechanics between those with tetra- and paraplegia. (Newsam, et al. 1999; Finley, et al. 2004). These studies used different wheelchair ergonometer setups to simulate propulsion; the frictional and inertial properties of each may have caused these discrepancies. Using an overground setup may better mimic the built environment and provide information that is more clinically-relevant (Cowan, Boninger, Sawatzky, Mazoyer, & Cooper, 2008).
The purpose of the present study was to investigate differences in wrist joint kinematics and kinetics between wheelchair users with paraplegia and tetraplegia during overground propulsion. A secondary purpose was to investigate how biomechanics varied when propelling over different surfaces at various speeds. It was hypothesized that wrist propulsive joint motions and forces would be greater in those with tetraplegia. Differences were hypothesized to be greatest during conditions with unnatural propulsion speeds and surfaces with high rolling-resistance (RR).
methods
Subject Recruitment
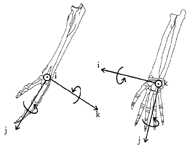 Figure 1. Axes of the wrist local coordinate system. Axis-j: force – compressive/distractive; rotation – pronation/supination. Axis-i: force – ulnar/radial shear; rotation – flexion/extension. Axis-k: forces – palm/dorsum; rotation – ulnar/radial deviation. Adapted from Boninger et al., 1997.
Figure 1. Axes of the wrist local coordinate system. Axis-j: force – compressive/distractive; rotation – pronation/supination. Axis-i: force – ulnar/radial shear; rotation – flexion/extension. Axis-k: forces – palm/dorsum; rotation – ulnar/radial deviation. Adapted from Boninger et al., 1997. Participants were recruited through research registries, flyers, and word of mouth. They were included if they were between 18 and 65 years of age; had an SCI with residual paralysis for over one year; used a manual wheelchair as their primary means of mobility; were injured after age 15; and were primarily English speaking. Exclusion criteria included history of upper-extremity fractures or dislocations that had not fully recovered; upper-limb dysthetic pain from a syrinx or regional pain syndrome; not having a “quick-release” axle; pregnancy; or history of cardiovascular or cardiopulmonary disease.
Baseline Questionnaires and Examinations
Ethical approval was provided by the appropriate Institutional Review Boards. After providing informed consent, participants provided demographic information and had their weights measured using a wheelchair scale.
Kinematic Data Collection
Participants propelled down a 15-meter runway over tile and medium-pile carpet at self-selected and targeted (1.5 meters/second) speeds. Five trials were performed per condition. A 20-camera VICON system captured the runway volume. Prior to propelling, participants were equipped with reflective markers on the acromion, trunk, medial and lateral epicondyles, ulnar and radial styloids, and 3rd metacarpal-phalangeal joint (Boninger, Cooper, Robertson, & Rudy, 1997); 8 additional markers in diamond-shaped patterns were added to the upper- and lower-arm. A SmartWheel, which detects handrim three-dimensional forces and moments (Cooper, Robertson, VanSickle, Boninger, & Shimada, 1997), was attached opposite a dummy wheel with identical handrim and treads.
| Demographics | PP (N=18) | TP (N=8) | p | ||
|---|---|---|---|---|---|
| M | SD | M | SD | ||
| Age (years) | 35.3 | 10.4 | 36.9 | 10.0 | .717 |
| DOI (years) | 13.3 | 8.9 | 11.2 | 8.5 | .574 |
| Weight (kg) | 75.5 | 20.8 | 69.8 | 18.8 | .513 |
| Gender | 13 Male 5 Female |
6 Male 2 Female |
1.00 | ||
| Ethnicity | 14 White 3 Black 1 Multiracial |
7 White 1 Black |
1.00 | ||
Notes. PP=paraplegia. TP=tetraplegia. DOI=duration of injury. |
|||||
Kinematic data were collected via VICON at 60 Hz and filtered using a 4th order zero-phase low-pass Butterworth filter with 7 Hz cutoff. Kinetic data were collected via the SmartWheel at 240 Hz and filtered using an 8th order zero-phase low-pass Butterworth filter with a 20 Hz cutoff frequency, then down-sampled to 60 Hz to match kinematics. Trials were split into start-up (first 3 strokes) and steady-state (all strokes after start-up).
A previously-described inverse dynamics model was created to transform handrim forces and moments to the wrist joint (Cooper, Boninger, Shimada, & Lawrence, 1999; Mercer et al., 2006). Handrim forces and moments were collected using a SmartWheel, then input into the model to calculate wrist joint reaction forces with respect to the global coordinate system. Kinetics were transformed to the wrist local coordinate system – the forearm. Joint coordinate systems and motions were defined as recommended by the International Society of Biomechanics (Figure 2; Wu, et al.
2005). Peak three-dimensional forces and motions were analyzed. Wrist compressive, ulnar/radial shear, and palm/dorsum shear forces were calculated from this model (Figure 2). Not all subjects ulnarly deviated or supinated their wrists, so radial deviation and pronation minimum and maximums were reported. Data from all steady-state strokes per trial were analyzed and averaged, and then all trials per condition were averaged.
Statistical Analysis
Significance was set a priori to α=.05. Normality was assessed using the Shapiro-Wilk test. Participants were dichotomized into those with paraplegia (T1 or below) or tetraplegia (C7 or above). Group demographic differences were tested using Fisher’s exact test (categorical) and independent t-tests (continuous). Between-subjects biomechanical differences were tested using two-way mixed analysis of variance. Independent variables included injury-level (between-subjects) and speed/surface condition (within-subjects). Dependent kinematic variables were peak wrist flexion, extension, maximum and minimum pronation and radial deviation, and ROM in each axis (Figure 2). Dependent kinetic variables included peak wrist resultant, compressive, palm to dorsum, and radial shear forces. To maximize statistical power with the small sample size it was decided not to apply corrections to these a priori tests. Following significant omnibus F-tests, univariate between-subjects ANOVAs were performed for each condition. Differences in velocity were also tested using two-way mixed ANOVA. Bonferonni corrections were applied to all post hoc tests.
| Surface-Speed | PP (N=18) | TP (N=8) | ||
|---|---|---|---|---|
| M | SD | M | SD | |
| Cement-SS | 1.63 | 0.28 | 1.70 | 0.30 |
| Cement-targeted | 1.66 | 0.14 | 1.67 | 0.38 |
| Carpet-SS | 1.47 | 0.23 | 1.55 | 0.38 |
| Carpet-targeted | 1.61 | 0.95 | 1.58 | 0.11 |
| Notes. PP: Paraplegia. TP: Tetraplegia. SS: Self-selected. A main effect of condition was found, F(1.771,42.508)=4.195, p=.026, partial η2=.149. Post hoc differences were observed between cement and carpet at self-selected (p=.039) and targeted speeds (p=.027). | ||||
Wrist forces correlated with body-weight (p<.05) and thus were weight-normalized. Velocities were different between surface/speed conditions (p<.05; Table 2). Wrist kinematics can change with variations in speed (Boninger et al., 1997), so joint motions were normalized to velocity.
results
| Surface-Speed | Paraplegia (N=18) | Tetraplegia (N=8) | F(1,24) | p | R2 | Adjusted R2 | ||
| Palm to Dorsum Forcea | ||||||||
| M | SD | M | SD | |||||
| Cement-SS | 0.43 (30.1) | 0.21 (13.7) | 0.55 (37.8) | 0.21 (14.0) | 2.105 | .160 | .081 | .042 |
| Cement-targeted* | 0.39 (28.8) | 0.09 (9.7) | 0.65 (44.8) | 0.28 (19.4) | 13.069 | .001 | .353 | .326 |
| Carpet-SS | 0.42 (32.2) | 0.13 (13.2) | 0.58 (41.0) | 0.17 (16.7) | 6.659 | .016 | .217 | .185 |
| Carpet-targeted* | 0.48 (35.4) | 0.12 (11.2) | 0.66 (46.5) | 0.21 (18.3) | 8.051 | .009 | .251 | .220 |
| Resultant Forceb | ||||||||
| Cement-SS | 0.78 (57.1) | 0.28 (21.0) | 0.99 (63.3) | 0.48 (15.5) | 2.088 | .161 | .080 | .042 |
| Cement-targeted | 0.74 (55.3) | 0.14 (15.7) | 1.08 (70.0) | 0.53 (24.2) | 6.561 | .017 | .215 | .182 |
| Carpet-SS | 0.84 (63.4) | 0.19 (22.5) | 1.01 (66.1) | 0.48 (22.3) | 1.811 | .191 | .070 | .031 |
| Carpet-targeted* | 0.86 (64.3) | 0.18 (19.1) | 1.15 (75.7) | 0.38 (17.1) | 7.392 | .012 | .235 | .204 |
| Flexion/Extension Range of Motionc | ||||||||
| Cement-SS | 0.78 (57.1) | 0.28 (21.0) | 0.99 (63.3) | 0.48 (15.5) | 6.113 | .021 | .203 | .170 |
| Cement-targeted | 0.74 (55.3) | 0.14 (15.7) | 1.08 (70.0) | 0.53 (24.2) | 5.650 | .026 | .191 | .157 |
| Carpet-SS | 0.84 (63.4) | 0.19 (22.5) | 1.01 (66.1) | 0.48 (22.3) | 1.801 | .192 | .070 | .031 |
| Carpet-targeted* | 0.86 (64.3) | 0.18 (19.1) | 1.15 (75.7) | 0.38 (17.1) | 12.782 | .002 | .348 | .320 |
| Notes. SS: Self-selected. *Significant after Bonferonni correction (p<.0125). aF(1,24)=10.727, p=.003, partial η2=.309. bF(1,24)=4.751, p=.039, partial η2=.165.cF(1,24)=6.552, p=.017, partial η2=.214. | ||||||||
Participants
Thirty-one manual wheelchair users were recruited. Three did not meet inclusion criteria and two had wrist data that could not be analyzed (both with paraplegia), leaving a sample size of 26. No demographic differences were found between groups (Tables 1). Injury levels of the participants with tetraplegia were C5 (N=2), C5/6 (N=1), and C7 (N=5).
Between-Subjects Effects
Omnibus F-tests indicated a main effect of injury-level on normalized flexion/extension ROM, FR, and palm to dorsum shear force (p<.05; Table 3). Post hoc univariate between-subjects F-tests indicated differences in peak ROM and FR (p<.0125; Table 3) on carpeted surfaces at targeted speed. Differences in palm to dorsum forces were significant on both cement and carpet at targeted speed (p<.0125; Table 3). Velocity differed between conditions (p<.05; Table 2), but not between injury-level groups.
discussion
Differences based on injury level were observed in wrist joint reaction forces and kinematics during propulsion over cement and carpeted surfaces. Participants with tetraplegia experienced greater wrist loading and ranges of motion. Reduced grip strength caused by upper-extremity paralysis may have required this group to compensate by applying more force and increasing friction between palm and handrim. Additionally, flexor and extensor motor imbalances may have contributed to the higher ROMs in the same group. These adaptations likely allow individuals with upper limb paralysis to attain a functional velocity. However, high forces may also contribute to the upper-extremity pain and injury observed (van Drongelen et al., 2006). Interventions that optimize hand and wrist biomechanics may improve function while decreasing risk of injury. These interventions could take the form of orthotics or special wheelchair components, such as pushrims that work to increase friction and/or wrist stability.
Of importance are the biomechanical differences observed over carpet and at targeted speeds. Carpet increases RR at the targeted speed and may elicit an unnatural propulsion technique. Indeed, propulsion biomechanics have been observed to change with variations in RR (Cowan, Nash, Collinger, Koontz, & Boninger, 2009). These conditions may have potentially amplified differences between injury levels. Boninger, et al. (1999) found RR influenced propulsive forces, and may contribute to median neuropathy. Further study is necessary to understand how propulsion over different surfaces impacts pathology. Flooring that reduces RR and facilitates low-force propulsion may improve accessibility.
This study utilized an overground setup to measure kinematics, in contrast to previous investigations that have used wheelchair ergometers (Newsam et al., 1999; Finley et al., 2004). Although the fixed setup offers advantages, frictional and inertial differences may have induced unnatural techniques that differ from propulsion over surfaces found in the built environment. For example, flexion/extension ROMs in this study’s tetraplegia group were higher than those from a previous study (Newsam et al. 1999). Finley et al. (2004) reported greater wrist forces than those in the current sample, and found significantly greater wrist joint forces in the group without upper limb impairment. It is possible the overground setup elicits a more natural technique that can compare to propulsion over surfaces found in the built environment. This may allow for results that are more clinically relevant and generalizable to the SCI population (Cowan et al., 2008).
Limitations
The sample size was disproportionate with respect to injury-level groups. This affected variability of the data and thus significance and generalizability of some of the tests. The laboratory setup, including VICON markers and the SmartWheel, may have altered natural propulsion style. Finally, the sample included highly independent wheelchair users who could complete a lengthy protocol. This is not characteristic of all wheelchair users with SCI and thus limits generalizability.
CONCLUSIONS
Differences existed in wrist kinematics between manual wheelchair users with tetraplegia and paraplegia. Participants with tetraplegia propelled with greater F/E ROM and wrist reaction forces. Differences were most prevalent in conditions that increased RR. Further testing is necessary to better understand how these differences impact the risk of injury. These finding also might help design interventions that could improve propulsion biomecanchics in individuals with tetraplegia.
REFERENCES
Barr, A. E., Barbe, M. F., & Clark, B. D. (2004). Work-related musculoskeletal disorders of the hand and wrist: epidemiology, pathophysiology, and sensorimotor changes. Journal of Orthopaedic & Sports Physical Therapy, 34(10), 610-627.
Cowan, R. E., Boninger, M. L., Sawatzky, B. J., Mazoyer, B. D., & Cooper, R. A. (2008). Preliminary outcomes of the SmartWheel Users’ Group database: a proposed framework for clinicians to objectively evaluate manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation, 89(2), 260-268.
Cowan, R. E., Nash, M. S., Collinger, J. L., Koontz, A. M., & Boninger, M. L. (2009). Impact of surface type, wheelchair weight, and axle position on wheelchair propulsion by novice older adults. Archives of physical medicine and rehabilitation, 90(7), 1076-1083.
Finley, M. A., Rasch, E. K., Keyser, R. E., & Rodgers, M. M. (2004). The biomechanics of wheelchair propulsion in individuals with and without upper-limb impairment. Journal of Rehabilitation Research and Development, 41(3B), 385-394.
Newsam, C. J., Rao, S. S., Mulroy, S. J., Gronley, J. K., Bontrager, E. L., & Perry, J. (1999). Three dimensional upper extremity motion during manual wheelchair propulsion in men with different levels of spinal cord injury. Gait & Posture, 10(3), 223-232.
Pentland, W. E., & Twomey, L. T. (1994). Upper limb function in persons with long term paraplegia and implications for independence: Part I. Spinal Cord, 32(4), 211-218.
van Drongelen, S., De Groot, S., Veeger, H. E. J., Angenot, E. L. D., Dallmeijer, A. J., Post, M. W. M., & Van Der Woude, L. H. V. (2005). Upper extremity musculoskeletal pain during and after rehabilitation in wheelchair-using persons with a spinal cord injury. Spinal Cord, 44(3), 152-159.
Wu, G., Van Der Helm, F. C., Veeger, H. E. J., Makhsous, M., Van Roy, P., Anglin, C., ... & Buchholz, B. (2005). ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: shoulder, elbow, wrist and hand. Journal of Biomechanics, 38(5), 981-992.
ACKNOWLEDGEMENTS
Funding was provided by VA Grant #B6252R. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship (Grant #1247842). Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the view of the National Science Foundation, Department of Veterans Affairs, or United States Government.