INTRODUCTION

Cerebral Palsy (CP) is a non-progressive disorder that affects cognitive and functional abilities. [3] It often leads to diminished gait performance, which, in its most extreme case, can completely impair one's ability to walk.

One common observation in CP patients is drop foot- a condition in which the foot does not properly rotate during the swing phase of walking. A person with drop foot cannot lift their entire foot when walking, resulting in little to no clearance between the toes and the ground, causing the toes to drag and inhibiting any regular motion.

One solution is providing proper foot support in the form of an Ankle Foot Orthoses (AFO). An AFO is used to restore walking ability by either keeping the peripheral joints in a range of motion that will reduce pathological reflex patterns or restricting motion the user would naturally perform incorrectly. [4] For example, the talus of the ankle is held to eliminate downward rotation caused by drop foot. [5] In terms of general walking improvement, an AFO specifically helps to improve gait kinematics, decrease user energy, [6] and facilitate the development of motor skills. Gait parameters improved are the range of motion of both the ankle and knee joints, as well as increased walking ease, speed, and stride length. [5]

There are a variety of AFO designs on the market including the solid AFO (SAFO), dynamic AFO (DAFO), floor reaction orthosis (FRO), posterior leaf spring (PLS) and the hinged AFO (HAFO). [4] AFO's also have varying mechanical complexity ranging between passive, semi-active, and active devices. [2] A passive AFO can store and release energy elastically and functions by physically holding the ankle complex around the correct position. Semi-active AFOs have some sensor function, and active devices incorporate active movement of the joint (i.e. exoskeleton).

AFO design optimization seeks maximum comfort, high resistance to mechanical failure, and sufficient support. One of the best ways to analyze the mechanical properties of a complex flexible mechanism is the process of finite element analysis (FEA). In this study, an educationl version of the software Fusion 360 (version 2.0.6670), was utilized to conduct an effective analysis used for design optimization.

There are several materials commonly used for AFO design. Some are sturdy and provide ankle-joint stability, but split or crack along pressure points with repeated use. Others are flexible and provide comfort while sacrificing ankle-joint stability. This study compared several thermoplastic materials for stress tolerance and deformation resistance.

One of the objectives of this study is to create an AFO with complex geometry by cutting and bending a plate of thermoplastic material. After the proper material and thickness of the plate were identified via the sensitivity FEA we designed a 2-dimensional AFO "unfolded" model in Fusion 360. The model was then converted via virtual folding into a 3-dimensional model that was used for a final FEA. In order to create the physical model, a laser-cutter was used to cut a thermoplastic resin sheet into the desired 2-dimensional shape. Afterward, the final 3-dimensional product was produced by bending along proper creasing lines.

The paper is organized as such: the Methods section describes how the AFO was designed, how the 3-dimensional model was created, how the FEA was performed, and the cost-effective process for making the physical AFO. The Results section presents the results of the simulations and the Discussion section explains their implications.

METHODS

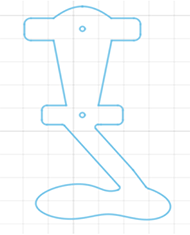
Overall, this study was comprised of four parts. First, a sensitivity analysis was performed to identify the best combination of material and plate thickness to fabricate an AFO. Second, an anterior support AFO virtual model was created as a planar cutout as shown in Figure 1. Third, using the material and thickness pairs selected in point one the planar model was extruded at the proper thickness, virtually folded, and underwent an FEA simulation. Finally, a physical model was created with a cost-effective manufacturing technique to demonstrate the feasibility of the manufacturing technique.

Description of the initial sensitivity analysis

A sensitivity analysis via FEA was performed to find the optimal material based on performance and cost. The simulation considered 11 thermoplastic polymeric materials and was run on a vertical cantilever beam (300mm x 50mm x T), with three different thicknesses "T" (i.e. 3mm, 6mm, and 9mm). The cantilever was fixed on one side, and a 100N force was applied to it, orthogonally to the length and width. The force was applied at the end of the cantilever, 300mm from the constraint. We consider this structural arrangement and loading scheme as a first approximation of the behavior of a user applying a load on an AFO during walking [7], without the necessity to deal with more complex geometry. This information and respective results can be viewed in Table 1. We performed this sensitivity analysis to find an optimal combination of material and plate thickness that would guarantee linear, yet large deformations. A combination of material and plate thickness with maximal deformation on the simplified model between 100 and 250mm indicate a secant angle between the constraint end of the cantilever and its free tip between 18 and 40 degrees, which is compatible with unimpaired dorsiflexion range in walking [8]. Many thermoplastic polymers can deform within such boundries without plasticising. Combination of materials and thickness passing this initial screaning were considered suitable to be tested in an FEA analysis with more complex geometry.

Constructing the 2-dimensional model of the AFO

To create the basis of the 2-dimensional design, there was a reference to TOEOFF® (Allard USA)- an orthosis similar to the desired design. To construct the footplate, geometrical reference points were placed on a sketching plane with appropriate dimensions based on the reference. Then, a spline curve tool was used to achieve the edges of the footplate (Figure 1). The upper structure of the AFO, composed of the ankle and shank support utilized the line, fillet, and dimension tools in Fusion 360. The final 2-dimensional drawing is displayed in Figure 1.

Constructing the 3-dimensional model of the AFO

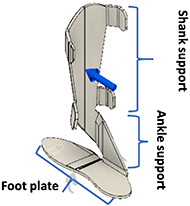
After the planar cutout was complete, it was transformed into a 3-dimensional model.

A 3-dimensional model was made using a sheet metal bending toolbox in Fusion 360's. The 2-dimensional drawing was thickened using Fusion 360's flange tool, as opposed to the more commonly used extrusion tool, and then bent into the shape of the AFO shown in Figure 2. It was bent at 90 degrees at the foot plate and then bent as needed to create a curvature in the shank and ankle support. This process was chosen because it allows to simulate the plastic deformation of the polymeric plate so to simulate the real fabrication process.

FEA Simulation

After the 3-dimensional design had been produced, the FEA simulation in Fusion 360 was carried out. Load configuration was based in part on a technique used in Zou et. al., indicating it is advisable to use a 100N force acting perpendicular and at half the height of the shank support to simulate a person walking with the AFO. [7] The centrod of the distributed force was located about 260mm above the foot plate. The toe region of the footplate was constrained to the ground. Simulations were performed on the entire 3-dimensional design 9 of the materials which pass our initial sensitivity analysis test.

Constructing the physical model

To create the physical model, the drawing of Figure 1 was imported into RDWorks 8.0 software, which sends a file to the laser cutter. A HL-Yeah 1060-130W laser cutter was used to shape the 2-dimensional model in a sheet of thermoplastic resin.

Once the 2-dimensional model was cut, a Wagner heat gun set to 1200 °F was used to warm the polymeric sheet until it was flexible enough to bend with moderate pressure on a 114.3 mm (4.5 inch) diameter metal cylinder. This achieved the curve of the shank support that would surround the user's anterior lower leg, as previously modelled in our 3-Dimensional CAD model.

Finally, the ankle support was bent at a 90 degree angle to the footplate. Once cooling was complete, the product was finished. The model is modified based on weak points determined by FEA and the analysis of other common orthoses. Weak points can be reinforced by layers of crosslinked thermoplastic sheets.

Table 1: sensitivity analysis of material vs thickness where bolded number are impossible solutions

Material	3mm	6mm	9mm	Material	3mm	6mm	9mm
Acetal Resin	849.7	108.2	32.4	Nylon Molybdenum Disulphide	856.4	108.6	32.45
Acrylonitrile butadiene styrene (ABS)	1106	140.8	42.12	Polyaryletherketone (PAEK)	2200	281.1	84.4
Acrylic	913.9	115.9	34.66	Pentachlorophenol (PBT) Plastic	265.2	33.99	10.23
Liquid crystal polymer (LCP) Plastic	176.1	22.33	6.673	Polyethylene High Density	2704	344	103.1
Nylon 6	909.8	115.4	34.48	Polystyrene High Impact	1304	165.7	49.62
Nylon 6/6	856.4	108.6	32.45

 

RESULTS

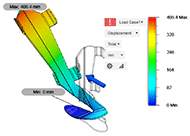
In this study, the optimal material/thickness combination can be defined as the solution of our sensitivity analysis where 1) the maximum deformation remains within the desired range of 100-250 mm, 2) the cost is lowest, and 3) the weight is lowest. Ultimately, 9 mm thickness models were not considered due to weight restrictions. Based on these parameters, the results in Table 1 demonstrate that the 6 mm thick model would work with the majority of the materials we selected., It can be seen that a 3mm plate would produce physically impossible results with deformation larger than the lenght of the cantilever for most materials except Liquid Crystal polymer (LCP) Plastic and Pentachlorophenol (PBT) Plastic.

The final set of simulations was performed on a geometrically complex model of the AFO with a 6 mm thickness and a 100 N applied force. Figure 4 shows the results of using ABS plastic, Figure 5 uses LCP plastic, and Figure 6 uses acetal resin. It is interesting to see how the design is able to support the progressive deformation of dorsiflexion (seen mostly in Figure 5) and toe extension (Figure 4 and Figure 6). This simulation was done to see if the design would properly deform given forces approximating to those likely to be created by the AFO's user. The total deformation and rotation of the toe-ankle complex allowed by each material is presented in Table 2, together with the rotational stiffness of the AFO.

Table 2: Deflection, Rotation and Stiffness for 6mm AFO.

Material	Deflection [mm]	Angle [deg]	Stiffness [Nm/deg]	Material	Deflection [mm]	Angle [deg]	Stiffness [Nm/deg]
Acetal Resin	315.1	50.47	0.52	Nylon 6/6	312.9	50.28	0.52
Acrylonitrile butadiene styrene (ABS)	408.4	57.52	0.45	Nylon Molybdenum Disulphide	312.9	50.29	0.52
Acrylic	334.5	52.14	0.50	Pentachlorophenol (PBT) Plastic	100.8	21.19	1.23
Liquid crystal polymer (LCP)  Plastic	64.34	13.90	1.87	Polystyrene High Impact	481.5	61.63	0.42
Nylon 6	332.9	52.01	0.50

DISCUSSION

Overall, the study was an economical approach to AFO design. The purpose of the FEA simulations was to see if the design performs its desired function of support by deforming within a desirable range when the force of walking is applied.The results show that the stiffness of an AFO can be properly set by the appropriate choice of material and thickness pairs. [9] Our analysis show that the stiffness of the AFO is well within the values of commertically available products that go from about 0.2Nm/deg aimed at users without dropfoot, [8] to 4.6 Nm/deg for stiffer carbon fiber AFO design for highly impaired individuals. [10] Finally, we demonstrated that the proposed manufacturing approach is feasible and could be scaled at the industrial level.